Intro and Linear Regression | Machine Learning
Intro and Linear Regression
Reference:
Introduction:
The defination of Machine Learning:
-
older: the field of study that gives computers the ability to learn without being explicitly programmed
-
Modern: A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E
Example: playing checkers.
E = the experience of playing many games of checkers
T = the task of playing checkers.
P = the probability that the program will win the next game.
Tool to used in this course: Matlab / Octave
Supervised Learning: Dataset with labels, know what our correct output should look like, having the idea that there is a relationship between the input and the output.
Regression problem: to predict results within a continuous output, meaning that we are trying to map input variables to some continuous function. Namely the price.
Classification problem: o predict results in a discrete output. In other words, to map input variables into discrete categories, like 0 and 1, true and fasle, 1/2/3/4/etc.
Unsupervised Learning: dataset without lables
Linear Regression with One Variable
Cost function: also called square error function, the function to return a number representing how well the neural network performed to map training examples to correct output.
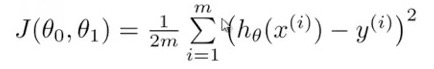
Gradient Descent: is a very popular learning mechanism that is based on a greedy, hill-climbing approach
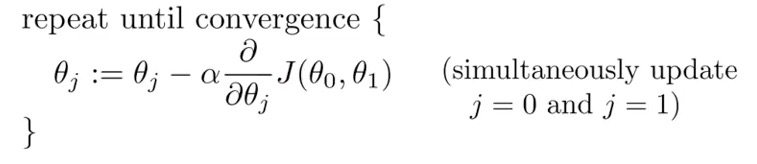alpha: learning rate
Batch Gradient Descent: each step of gradient descent use all the training examples.
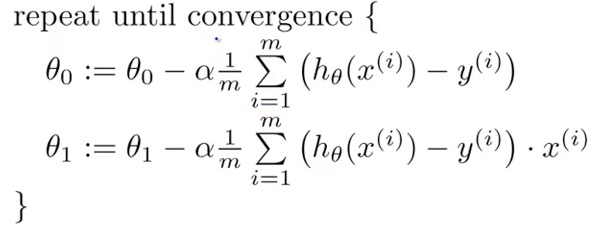
Convex function： （Bowl-shaped function）
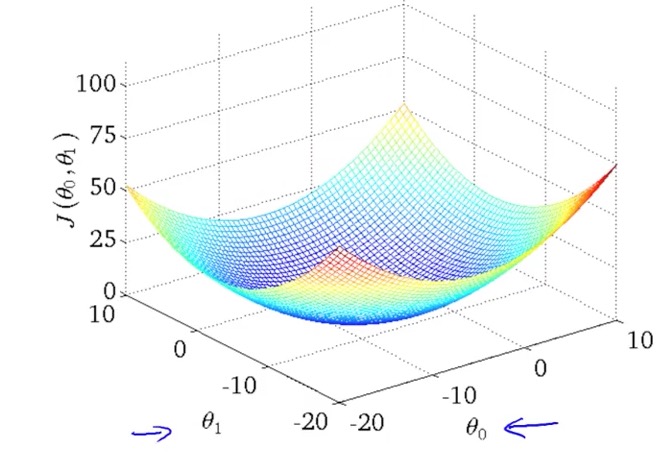
Linear Regression with Multiple Variables
gradient descent for multiple variables
mean normalization: keep the x -1 ≤ x ≤ 1, just the formula to narrow the values:
x¡ = (x - mean of x) / (range of x, maxium of x - minium of x)
feature and ploynomial regression: to choose the suitable features
Feature Scaling: is a method used to standardize the range of independent variables or features of data. In data processing, it is also known as data normalization and is generally performed during the data preprocessing step.
Learning Rate: if learning rate alpha is too small, slow convergence if too large, J(ø) may not decrease on every interation; may not converge.
q&A:
avg distance range value
89 81 8 25 0.32
72 81 -9 25 -0.36
94 81 13 25 0.52
69 81 -12 25 -0.48
avg distance range value
7921 6675.5 1245.5 4075 0.305644172
5184 6675.5 -1491.5 4075 -0.36601227
8836 6675.5 2160.5 4075 0.530184049
4761 6675.5 -1914.5 4075 -0.469815951
Gradient Descent:
need to choose alpha
need many iterations
work well when n is large
Normal Equation:
don't need to chosose alpha
don't need to to iterate
need to computer (n*n)
slow if n is very large
Octave Tutorial
Octave Document: