Octave简单使用说明
安装
基础操作
octave可以直接进行计算
2+2
2*2
octave已经内置了常用的数学函数,函数名字比较通用,cos, sin,log, log10, abs,round等
使用上下箭头显示历史指令
使用help显示帮助
使用分号隐藏结果
基础操作符号
可以使用PS1指令简化现实: PS1('>> ')
加减乘除: + - * /
与或非: && || XOR
变量
Octave中变量是不需要声明就可以赋值使用;注意
a = 3
a=pi
disp(sprintf('2 decimals: %0.2f', a))
可以使用format指令调整数值显示的不同样式
format long
format short
显示变量
who % show the variables in scope
whos % show the variables in scope with more detail info
清除变量
clear
clear v
文件处理
使用pwd显示当前路径,load加载文件,save将变量保存到文件
pwd % path of current folder
load file.dat
load('file.dat')
save hello.dat v
save hello.txt v --ascii % save as text ascii
矩阵处理
对于矩阵也可以直接赋值,也可以使用zeros,ones,rand, eye, diag等内置函数生成
A = [1 2; 3 4; 5 6]
v = [1 2 3] % three one vector
v = [1; 2; 3] % one-three vector
v = 1:0.1:2 % by step .1 from 1 to 2
v = 1:6
w = rand(1,3) % randon number of one by three vector
w = rand(1,3) % negative
w = -6 + sqrt(10)*(randn(1, 10000)
D = eye(4) % 单位阵,D(i,i)为1,其他为零
B = diag([-1, 7 2]) % 对角线为参数的值
获取矩阵大小和长度
size(A)
size(A, 1)
lenth(A) % return the longer vector
矩阵处理
A(2,:) % ":" means every elements along that row/column
A(:,2)
A([1 3],:)
A = [A, [100, 100, 102]] % append another column vector to right
A(:) % put all elements of A into a single vector
C = [A B]
C = [A; B] % ; mean next line
C = [A, B]
矩阵转置符 ‘
A = [1 2 3; 4 5 6]
A'
ans =
1 4
2 5
3 6
矩阵计算
简单对普通变量作加减乘除直接对矩阵中每个变量作处理,比如 *2 对每个变量都做乘2处理
矩阵之间的乘除按照矩阵的计算规则,一般矩阵乘法中矩阵大小为
(l × m) ∗ (m × n) → (l × n)
如果机算符前的‘.’表示为一个元素对元素的计算
A = eye(5)
B = ones(5)
A * B %矩阵乘法
A .* B %注意每个算符前的‘.’表示为一个元素对元素的计算
一些内置函数可以对矩阵直接进行计算
inv % 求矩阵逆矩阵
det % 求矩阵特征值
trace % 求矩阵的迹
eig % 求矩阵的特征向量和特征值
图形显示
提示:如果调用画图函数出错有可能是gnuplot配置不正确或者缺少组件,这时候可以选择重新安装gnuplot及其所需组件。
基本用法
常用的画图函数:plot, hist
angles = linspace(0,2*pi,100);
y= sin(angles);
plot(angles, y);
增强图形,添加图片名称和x/y轴名称
title('Graph of y=sin(x)');
xlabel('Angle');
ylabel('Value');
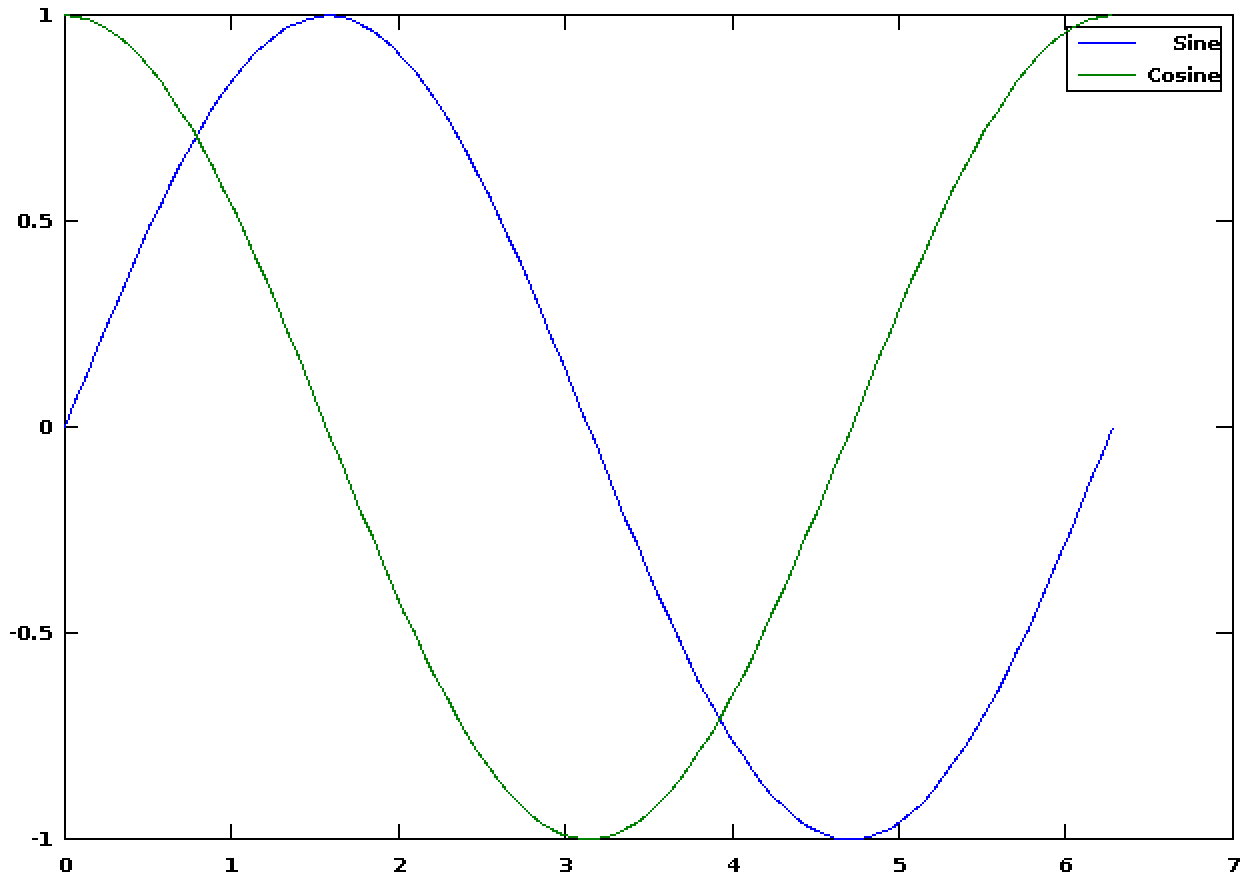
也可以画多条曲线,可以用legend设置曲线名称
z = cos(angles);
plot(angles, y, angles, z);
legend('Sine', 'Cosine');
其他图形函数
w = eye(5);
hist(w)
hist(w, 50)
多个图形可以通过figure命令来切换/控制
图形可以通过print指令打印或者保存为文件,支持pdf,png,jpg,gif,ps,eps等
print('graph1.png','-dpng')
print -djpg figure2.jpg
高级用法
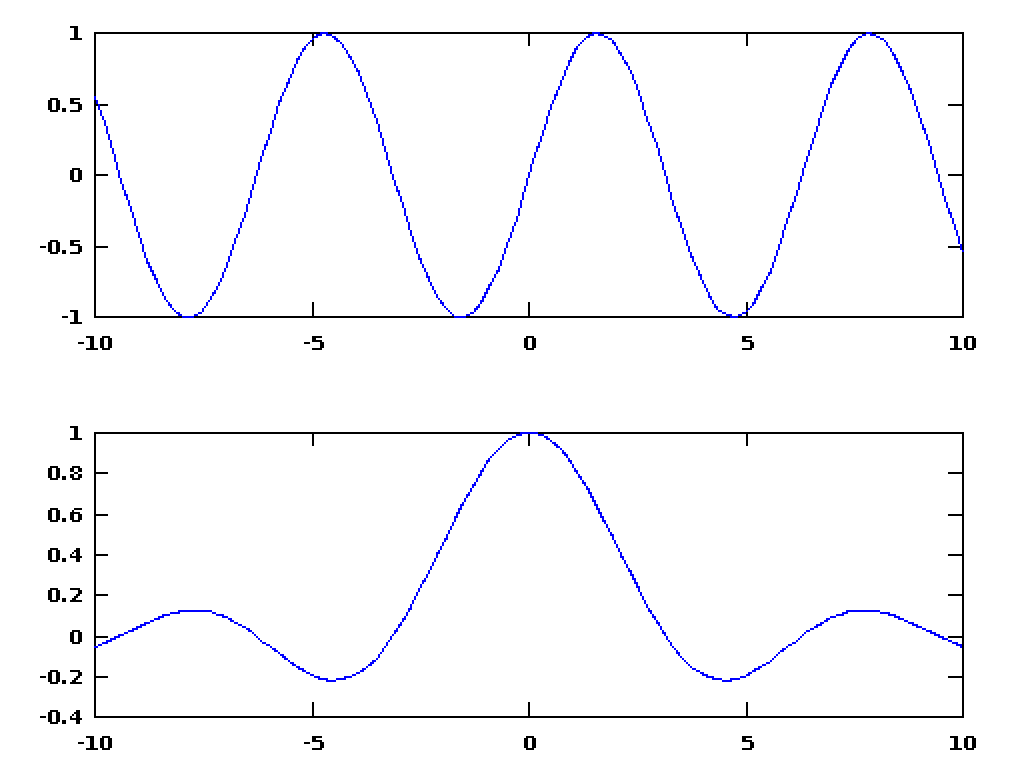
使用subplot创建子图
x=linspace(-10,10);
subplot(2,1,1)
plot(x,sin(x));
subplot(2,1,2)
plot(x,sin(x)./x)
使用plot3做3D画图)
z = [0:0.05:5];
plot3 (cos(2*pi*z), sin(2*pi*z), z, ";helix;");
3D曲面
% 初始化一个网格点
x=2:0.2:4;
y=1:0.2:3;
[X,Y]=meshgrid(x,y);% make the grid
% 使用二元函数 f(x,y)=(x−3)^2 −(y−2)^2
Z=(X-3).^2-(Y-2).^2;
subplot(2,2,1);surf(Z);title('surf')
subplot(2,2,2);mesh(Z);title('mesh')
subplot(2,2,3);meshz(Z);title('meshz')
subplot(2,2,4);contour(Z);title('contour')
Octave编程
选择 if… else, switch
if conditionA
doSomething
else
doSomethingElse
end
switch variableA
case conditionA
doTaskB
case condtionB
doTaskB
otherwise
doSomethingElse
end
循环 for, while
for n=1:5
nf(n)=factorial(n);
end
while conditionWhile
doWhile
end
函数
Octave函数中阐述是通过值传递的;每个函数的第一行要标明函数名和参数;文件名不必和函数名一致
function [output1,output2,...]=name(input1,input2,...)
function s=sind(x)
% SIND(x) Calculates sine(x) in degrees
s=sin(x*pi/180);
endfunction
附录1: 矩阵运算规则
矩阵和数的加减乘除
矩阵中的每个元素都对数进行同意的加减乘除操作
比如 A = ones(5,5), A - 1 = zeros(5, 5)
矩阵的加法/减法
两个矩阵相加减,即它们相同位置的元素相加减!
注意:只有对于两个行数、列数分别相等的矩阵(即同型矩阵),加减法运算才有意义,即加减运算是可行的.
矩阵的加减法满足交换律和结合律
* 交换律 A + B = B + A
* 结合律 (A + B) + C = A + (B + C)
矩阵和矩阵的乘法
设A为(M*x)矩阵,B为(y*N),则A与B的乘积C=A*B是这样一个矩阵:
(1) 行数与(左矩阵)A相同,列数与(右矩阵)B相同,即C为(M*N)矩阵.
(2) C的第i行第j列的元素C(i,j)由A的第i行元素与B的第j列元素对应相乘,再取乘积之和.
只有左矩阵的列数=右矩阵的行数的时候矩阵乘法才是可行的,即 M=N
矩阵和单位阵相乘等于自身。单位阵为octave里面eye函数生成的矩阵,一般用E表示,(i, i)元素为1, 其他为零,地位类似于数值中的1
两个非零矩阵的乘积可以是零矩阵.由此若A * B = 0,不能得出A = 0或 B = 0的结论.
矩阵乘法不满足交换律
满足结合律[(A * B) * C = A * (B * C)]和分配律 A * (B + C) = A * B + A * C
矩阵转置
将矩阵A的行换成同序号的列所得到的新矩阵称为矩阵A的转置矩阵,记作A’
如果 A’ = A, 则A为对称矩阵,它的元素以主对角线为对称轴对应相等